1. Bells 101
To get into the Christmas spirit I thought I’d write a post about the Bell numbers. The Bell numbers ![]() count the number of partitions of a set of size
count the number of partitions of a set of size ![]() where a partition means what you would guess it does: a decomposition of the set into disjoint non-empty parts. In detail, writing
where a partition means what you would guess it does: a decomposition of the set into disjoint non-empty parts. In detail, writing ![]() , we say
, we say ![]() form a partition of
form a partition of ![]() if they are disjoint (that is
if they are disjoint (that is ![]() for all
for all ![]() ), cover
), cover ![]() (that is
(that is ![]() ) and are non-trivial (
) and are non-trivial (![]() for all
for all ![]() ). Again surprising no one, given such a partition, we call the
). Again surprising no one, given such a partition, we call the ![]() the parts.
the parts.
While there are plenty of things we could ask about partitions I’m solely interested here in counting how many partitions there are of ![]() , calling this the
, calling this the ![]() th Bell Number and written
th Bell Number and written ![]() . Specifically I’m interested in getting an idea of how quickly
. Specifically I’m interested in getting an idea of how quickly ![]() grows with
grows with ![]() and to this end will be trying to find some half-decent bounds on
and to this end will be trying to find some half-decent bounds on ![]() .
.
2. The motivating problem
Last year I found myself discussing the following problem with one of my students (after they had their supervision I might add!) from one of their problem sheets — but perhaps I won’t say which lest I give students an easy way to spoil a question for themselves. It asked students to prove two bounds on the Bell numbers (though the question was stated in terms of counting equivalence relations).
Specifically they were asked to show that
![]()
Where might these bounds come from?
Well the left hand side is ![]() , or half the number of subsets of
, or half the number of subsets of ![]() — perhaps that gives a clue? Given any single subset of
— perhaps that gives a clue? Given any single subset of ![]() we can define a partition by taking it and its complement as the two parts (I suppose strictly if one is empty we take the whole of
we can define a partition by taking it and its complement as the two parts (I suppose strictly if one is empty we take the whole of ![]() as the only part). But then of course every such partition arises in this way exactly twice since initially choosing a subset or its complement generates the same bipartition (again I’m lying here in the case that the set or its complement is empty). So there certainly are at least
as the only part). But then of course every such partition arises in this way exactly twice since initially choosing a subset or its complement generates the same bipartition (again I’m lying here in the case that the set or its complement is empty). So there certainly are at least ![]() such partitions.
such partitions.
On the other hand the right hand side is ![]() — the number of subsets of all (unordered) pairs in
— the number of subsets of all (unordered) pairs in ![]() . So what could choosing a collection of pairs have to do with counting partitions? Well this is where the equivalence relation perspective is useful: every partition corresponds to a unique equivalence relation and an equivalence relation is just a collection of unordered pairs with some extra restrictions. If you haven’t seen equivalance relations before then instead given a partition generate a unique collection of pairs in
. So what could choosing a collection of pairs have to do with counting partitions? Well this is where the equivalence relation perspective is useful: every partition corresponds to a unique equivalence relation and an equivalence relation is just a collection of unordered pairs with some extra restrictions. If you haven’t seen equivalance relations before then instead given a partition generate a unique collection of pairs in ![]() by including every pair of elements in the same part. But there are
by including every pair of elements in the same part. But there are ![]() ways of choosing a collection of pairs in any way whatsoever, so certainly there can be at most this many partitions.
ways of choosing a collection of pairs in any way whatsoever, so certainly there can be at most this many partitions.
So there we are: we’ve got both bounds. The original question however went on to ask: “can you give a stronger upper bound?”. For the rest of this post we’ll give a few refinements to both bounds until we hopefully come away with a reasonable idea how big ![]() is.
is.
2.1. A cheap upper bound
So far then we have
![]()
We’d like to avoid a can’t-see-the-wood-for-the-trees situation and so introduce a little bit of notation to allow us to state the results with a little less precision but without too much extraneous information. We write ![]() for something which goes to zero as
for something which goes to zero as ![]() goes to infinity. So for example since we have
goes to infinity. So for example since we have
![]()
and of course ![]() we can write
we can write
![]()
This allows us to discard a bit of the nuance of the error terms and write our bounds so far as
![]()
There’s clearly quite a gap.
It turns out it’s not actually as hard as you’d expect to get a pretty substantial improvement on the upper bound. Indeed we already know how to calculate partitions with extra structure. If we cyclically order each of the parts then we would get a partition and there are ![]() of those. This is a pretty substantial improvement. Indeed it gets the upper bound down to:
of those. This is a pretty substantial improvement. Indeed it gets the upper bound down to:
![]()
Now since ![]() is superexponential, or in other words
is superexponential, or in other words ![]() grows faster than linearly, our next objective might as well be to try and find a superexponential lower bound on
grows faster than linearly, our next objective might as well be to try and find a superexponential lower bound on ![]() (or superlinear bound on
(or superlinear bound on ![]() ).
).
2.2. Ripping off the last lower bound
Here the idea behind the last lower bound gives a good idea of how we might make some improvements. Once we’ve chosen a subset, why just take what’s left as the other part when we could partition what’s left? Sure this doesn’t give an explicit bound, but it could give us a way to lower bound ![]() in terms of
in terms of ![]() for some values of
for some values of ![]() smaller than
smaller than ![]() .
.
For instance, if we fix the size of the set we choose in the first instance as ![]() then the number of ways we can partition what’s left over is just
then the number of ways we can partition what’s left over is just ![]() . The slight wrinkle in this plan is that one of the parts we chose in the partition of the
. The slight wrinkle in this plan is that one of the parts we chose in the partition of the ![]() elements left over could have size
elements left over could have size ![]() and then we could have ended up with the same partition by choosing that subset as the initial subset of size
and then we could have ended up with the same partition by choosing that subset as the initial subset of size ![]() . This issue can be sidestepped by just insisting that we always include a fixed element, say 1, in the initial part or subset and selecting say
. This issue can be sidestepped by just insisting that we always include a fixed element, say 1, in the initial part or subset and selecting say ![]() other elements to place in the part with it from among the
other elements to place in the part with it from among the ![]() elements which aren’t 1. Then we get
elements which aren’t 1. Then we get
![]()
Even for moderately small ![]() this gives an improvement on what we had before. Say for example if we take
this gives an improvement on what we had before. Say for example if we take ![]() then we get
then we get
![]()
That is to say compared to our lower bound ![]() in which we pick up a factor of 4 when
in which we pick up a factor of 4 when ![]() is increased by 2, from this bound we see that we actually pick up at least a factor of
is increased by 2, from this bound we see that we actually pick up at least a factor of ![]() . We’re ultimately not too concerned by exactly what we can get out of the
. We’re ultimately not too concerned by exactly what we can get out of the ![]() case. However, since it will serve as a nice warm up for what we will do next we give some of the details. Before doing this it’s worth pointing out that since we get a factor of
case. However, since it will serve as a nice warm up for what we will do next we give some of the details. Before doing this it’s worth pointing out that since we get a factor of ![]() going from
going from ![]() to
to ![]() , the best lower bound we could get from this can’t be better than
, the best lower bound we could get from this can’t be better than ![]() .
.
On the other hand, suppose we had ![]() for some
for some ![]() (that is we pretty much have the
(that is we pretty much have the ![]() bound for
bound for ![]() , but just for a fraction slightly less than
, but just for a fraction slightly less than ![]() ) then our recursive bound would give
) then our recursive bound would give
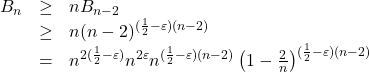
simply by breaking the exponent of ![]() up as
up as ![]() and writing
and writing ![]() . But then
. But then
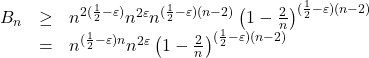
by collecting terms. And this in turn exceeds ![]() for sufficiently large since
for sufficiently large since ![]() and
and ![]() as
as ![]() . All this is to say that we can prove a lower bound of the shape
. All this is to say that we can prove a lower bound of the shape ![]() by induction once it actually starts to be true. The good news is that for any
by induction once it actually starts to be true. The good news is that for any ![]() and any fixed number of
and any fixed number of ![]() there has to be a constant
there has to be a constant ![]() such that the bound
such that the bound ![]() holds and thereafter the argument above shows that this bound will hold for all
holds and thereafter the argument above shows that this bound will hold for all ![]() by induction.
by induction.
Clearly even for ![]() we could do a bit better than this. Indeed the previous argument only actually requires of
we could do a bit better than this. Indeed the previous argument only actually requires of ![]() that
that ![]() . But the overall improvement is pretty small fry compared to what we can pull off with a similar amount of laziness for larger (but bounded) values of
. But the overall improvement is pretty small fry compared to what we can pull off with a similar amount of laziness for larger (but bounded) values of ![]() .
.
So far then we have
![]()
By looking at bounded ![]() it’s possible to show that
it’s possible to show that
![]()
Indeed we have
![]()
Now for ![]() bounded
bounded ![]() so
so ![]() (in fact the error term here is
(in fact the error term here is ![]() ). Moreover as
). Moreover as ![]() bounded, while it is potentially quite large we do certainly know that
bounded, while it is potentially quite large we do certainly know that ![]() is bounded in
is bounded in ![]() . At this point it would be handy to introduce a little bit of new notation.
. At this point it would be handy to introduce a little bit of new notation.
You’ll remember that in the ![]() case there was a huge amount of slack. Indeed it wouldn’t have mattered if there were some (even potentially very small) constants (that is maybe depending on
case there was a huge amount of slack. Indeed it wouldn’t have mattered if there were some (even potentially very small) constants (that is maybe depending on ![]() but not on
but not on ![]() ) kicking around since we had a factor of
) kicking around since we had a factor of ![]() in there which went to infinity with
in there which went to infinity with ![]() . With this in mind we write
. With this in mind we write ![]() when the bound holds but perhaps up to a multiplicative constant.
when the bound holds but perhaps up to a multiplicative constant.
Thus we have
![]()
and from here the argument is much as in the ![]() case. For completeness’ sake I include it below, but if you’re trusting then feel free to skip ahead. Since we’re picking up
case. For completeness’ sake I include it below, but if you’re trusting then feel free to skip ahead. Since we’re picking up ![]() when going from
when going from ![]() to
to ![]() , that is incrementing the subscript
, that is incrementing the subscript ![]() times, we’re expecting to get something around
times, we’re expecting to get something around ![]() but certainly no better. As before we can proceed by induction supposing that
but certainly no better. As before we can proceed by induction supposing that ![]() for some
for some ![]() then our recursive bound would give
then our recursive bound would give
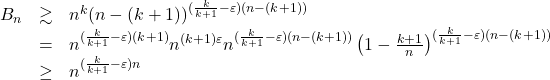
for ![]() sufficiently large as
sufficiently large as ![]() and
and ![]() as
as ![]() . As in the last case we could get away with
. As in the last case we could get away with ![]() .
.
3. Taking stock
All in all then we’ve made pretty decent progress, going from
![]()
or slightly more loosely
![]()
to
![]()
That is to say we know that up to lower order terms ![]() is
is ![]() , in the sense that their ratio tends to 1. It all looks a bit too good to be true really, but as always the devil is in the details and it turns out that the error terms we have are quite far apart. By Sterling’s formula we know that
, in the sense that their ratio tends to 1. It all looks a bit too good to be true really, but as always the devil is in the details and it turns out that the error terms we have are quite far apart. By Sterling’s formula we know that
![]()
whereas the situation with error term in the lower bound is a little less clear. Strictly what we showed was that for any ![]() satisfying
satisfying ![]() there exists a
there exists a ![]() such that
such that ![]() for all
for all ![]() . So without going to the trouble of working out how the constant depends upon the choices of
. So without going to the trouble of working out how the constant depends upon the choices of ![]() and
and ![]() we don’t really get any useful qualitative information on the error term in the lower bound. That is we have
we don’t really get any useful qualitative information on the error term in the lower bound. That is we have
![]()
The plan for next time then is try to work out how big ![]() is.
is.
Merry Christmas!
